Saltar al contenido
Control Automático Educación
Sistemas Dinámicos Lineales

Función de Transferencia y Variables de Estado

Continuamos viendo un poco más sobre la temática de sistemas dinámicos lineales y en esta ocación vamos a ver como se representan por Función de Transferencia y Variables de Estado estos sistemas. Adicionalmente veremos como transformar de una representación a otra.

Contenidos ocultar
1. Función de Transferencia y Variables de Estado
1.1. Función de Transferencia (Entrada – Salida)
1.2. Variables de Estado
2. Representación Función de Transferencia
3. Representación Variables de Estado
3.1. Realización Balanceada – Equilibrada – Valores Singulares de Hankel
3.2. Gramianos de Controlabilidad y Observabilidad
3.3. Transformacion de Similitud en Espacio de Estados
4. Ejemplos de representación en variables de estado
4.1. Péndulo
4.2. Péndulo Invertido

Antes de comenzar, te hago la invitación de que veas nuestro CURSO GRATUITO DE SISTEMAS DINÁMICOS LINEALES.

Función de Transferencia y Variables de Estado

Las dos representaciones mas utilizadas para describir los sistemas dinámicos lineales e invariantes en el tiempo son conocidas como la función de transferencia (entrada – salida) y las variables de estado (espacio de estados).

Estos tipos de representación pueden resumirse matematicamente de la siguiente forma:

Función de Transferencia (Entrada – Salida)

La función de transferencia es la representación de la teoría de control clásica con la cual podremos saber y determinar como es el comportamiento de un proceso o un sistema cualquiera. En una entrada anterior detallamos minuciosamente el concepto, junto con ejemplos sobre lo que representa y lo que es una función de transferencia.

Resumiendo un poco el concepto, debemos entender que una función de transferencia es un medio matemático que me relaciona la salida del proceso con respecto a la entrada y esta es representada a través del teorema de la convolución

y=\int_{0}^{t}G(t-\tau )u(\tau )d\tau\ \ \ (1)

Variables de Estado

Las variables de estado o espacio de estados son la representación de cualquier sistema o proceso empleados por la teoría del control moderno. Este tipo de representación en variables de estado brinda mucha más información dinámica del sistema, y si estas interesado (a) en conocer más sobre el espacio de estados, tenemos una entrada que explica al detalle las diferencias y el porque usar variables de estado en control.

Como concepto básico, podemos ver que la representación en espacio de estados es representado matricialmente por 4 elementos

\left\{\begin{matrix} \dot{x}(t)=Ax(t)+Bu(t) & \\ y(t)=Cx(t)+Du(t) & \end{matrix}\right.
  • A= Matriz dinámica
  • B= Matriz de control
  • C= Matriz de lectura
  • D= Matriz de paso

Representación Función de Transferencia

Normalmente usamos la representación de función de transferencia o entrada salida en el dominio transformado, aplicando la transformada de Laplace.

Por definición de cálculo, la transformada de laplace viene representada por la siguiente integral:

y(s)=\int_{0}^{\propto }y(t)e^{-st}dt

Aplicando la transformada de Laplace a la ecuación integral (1) se llega a la siguiente expresión algebraica, suponiendo que el sistema es monovariable (SISO). Es decir que tiene una entrada y una salida:

\hat{y}(s)=\hat{g}(s)\hat{u}(s)

Donde

\hat{g}(s)=\int_{0}^{\propto }g(t)e^{-st}dt
\hat{u}(s)=\int_{0}^{\propto }u(t)e^{-st}dt

Si el sistema no posee retardo (o sea que es totalmente racional), la función de transferencia g(s) es una función racional en s.

\hat{g}(s)=\dfrac{N(s)}{D(s)}=\dfrac{\beta _0s^m+\beta _1s^{m-1}…\beta _{m-1}s+\beta _m}{s^n+\alpha _1s^{n-1}…\alpha _{n-1}s+\alpha _n}

De acuerdo a los grados de los polinomios N(s) y D(s) una función de transferencia g(s) puede ser clasificada de la siguiente forma.

  1. n≥m, g(s) es propia.
  2. n>m g(s) es estrictamente propia
  3. n=m, g(s) es bi-propia
  4. n<m, g(s) no es propia

Representación Variables de Estado

Por otro lado aplicando la transformada de Laplace a la representación por variables de estado, se puede encontrar una relación directa entre las dos representaciones. Es decir podremos convertir de variables de estado para función de transferencia.

Considere la siguiente representación por variables de estado.

\left\{\begin{matrix} \dot{x}(t)=Ax(t)+Bu(t) & \\ y(t)=Cx(t)+Du(t) & \end{matrix}\right.

Considerando que x(s)=L\left \{ x(t) \right \} se obtiene que

\left\{\begin{matrix} s\hat{x}(s)=A\hat{x}(s)+B\hat{x}(s) & \\ \hat{y}(s)=C\hat{x}(s)+D\hat{x}(s) & \end{matrix}\right.
\hat{x}(s)=\left ( sI_n-A \right )^{-1}Bu(s)
\hat{G}(s)=\frac{y(s)}{u(s)}=C\left ( sI_n-A \right )^{-1}B+D

Cabe resaltar que la mayoría de los sistemas físicos son descritos por sistemas no lineales e variantes en el tiempo.

En general un sistema no lineal puede ser descrito por la siguiente representación en variables de estado

\left\{\begin{matrix} \dot{x}(t)=f(x(t),u(t),t) & \\ y(t)=h(x(t),u(t),t) & \end{matrix}\right.

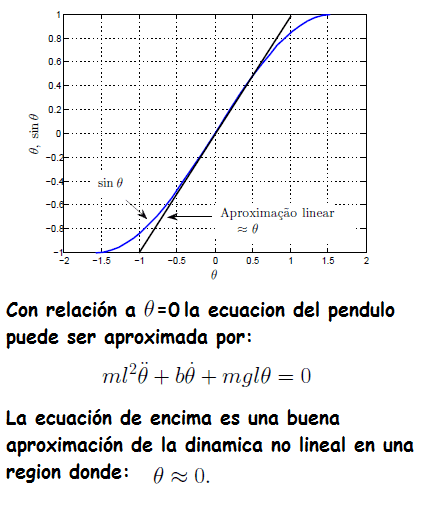
Sin embargo se puede aproximar un sistema NO lineal a través de un sistema lineal aproximado en torno a un punto de equilibrio. Esto lo hemos tratado en detalle en el CURSO GRATUITO DE ANÁLISIS DE SISTEMAS.

Ejemplos de representación en variables de estado

Vamos a ver algunos ejemplos de sistemas físicos reales, los cuales son sistemas NO lineales y deben linealizarse cerca de un punto de equilibrio para posteriormente poderlos representar a través de variables de estado lineales, para el estudio de sistemas LTI (Lineales e Invariantes en el Tiempo)

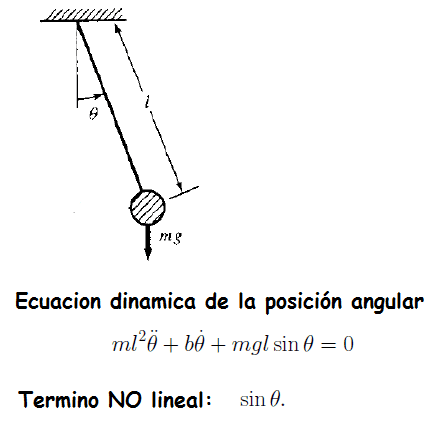
Péndulo

Veamos un ejemplo de aproximación lineal considerando un sistema de péndulo.

pendulo
aproximacion

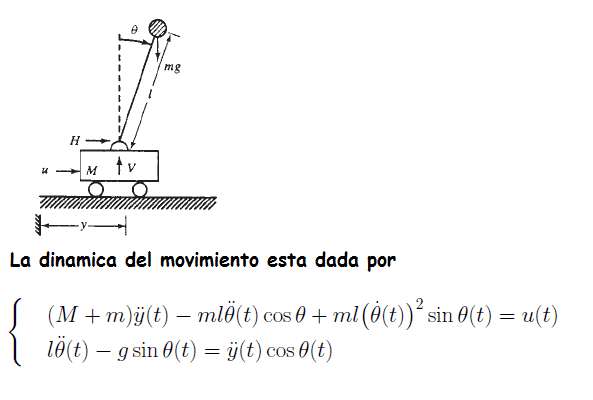
Péndulo Invertido

Considere el siguiente sistema de un péndulo invertido.

Pendulo Invertido

Hipotesis del sistema dinámico:

  • Linealizando en torno al punto θ=0
  • senθ≈θ y cosθ≈1
  • Considerando las funciones lineales apenas en θ(t) y θ̇(t)
(1)\ (M+m)\ddot{y}(t)-ml\ddot{\theta }(t)=u(t)
(2)\ l\ddot{\theta }(t)-g\theta(t)=\ddot{y}(t)

Reemplazo 2. en 1.

(M+m)(l\ddot{\theta }(t)-g\theta(t))=u
Ml\ddot{\theta }(t)=(M+m)+g\theta(t)+u
(3)\ \ \ddot{\theta}=\frac{M+m}{Ml}g\theta+\frac{u}{Ml}

Reemplazo 3. en 2.

(4)\ \ \ \ddot{y}=\frac{m}{M}g\theta+\frac{u}{M}

Determino las variables de estado

x_1(t)=y(t)\\x_2(t)=\dot{y}(t)\\x_3(t)=\theta(t)\\x_4(t)=\dot{\theta}(t)

Ecuaciones diferenciales del sistema

\dot{x}1(t)=x2(t)\\\dot{x}2(t)=\ddot{y}(t)=\frac{m}{M}gx3+\frac{u}{M}\\\dot{x}3(t)=x4(t)\\\dot{x}4(t)=\ddot{\theta}(t)=\frac{M+m}{Ml}gx3+\frac{u}{Ml}

El sistema representado por variables de estado queda:

\dot{x}(t)=\begin{bmatrix} 0 & 1& 0& 0\\ 0 & 0& \frac{mg}{M}& 0\\ 0 & 0& 0& 1\\ 0 & 0& \frac{M+m}{Ml}& 0 \end{bmatrix}x(t)+\begin{bmatrix} 0\\ \frac{1}{M}\\ 0\\ \frac{1}{Ml} \end{bmatrix}u(t)\\ y(t)=\begin{bmatrix} 1 & 0& 0& 0 \end{bmatrix}x(t)+\begin{bmatrix} 0 \end{bmatrix}u(t)

Eso es todo por la entrada del dia de hoy, espero les haya gustado y hayan aprendido algo nuevo. Si te ha servido el contenido de esta entrada, de los videos y los códigos de implementación y deseas apoyar mi trabajo invitandome a un café super barato, puedes hacerlo en el siguiente link:

👉 Invitar a Sergio a un Café ☕️

Que esten muy bien, nos vemos en la siguiente entrada.

Volver al Curso de Sistemas Dinámicos Lineales