Arduino

Como Hacer un Control PID de Temperatura con Arduino

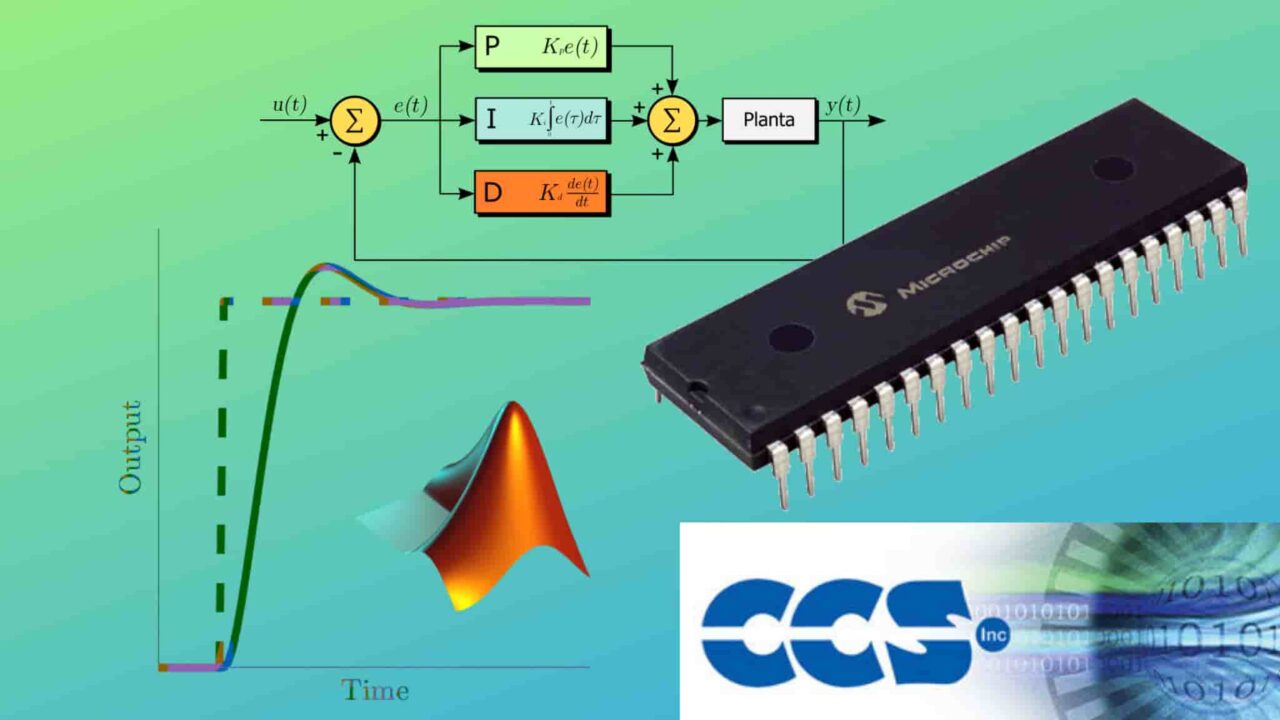
El control PID es el compensador más popular empleado en la mayoría de proyectos de control a nivel mundial y en esta entrada vas a aprender a programar tu propio Control PID sencillo de Temperatura con Arduino y Matlab o con el serial plotter. Sin embargo, puedes extenderlo para cualquier otra variable que desees controlar.

Contenidos ocultar

1. ¿Que es el controlador PID?

2. Control PID en Arduino

2.1. Curso Implementado en ARDUINO

2.2. Curso Implementado en Microcontrolador PIC

3. Controlador PID Discreto en Arduino

3.1. Medidor de Nivel de Agua por Presión con Arduino

3.2. Modelo Matemático de un Sistema Térmico

3.3. Relevador con Arduino

4. Planta de Temperatura

5. Identificación del Modelo de la Planta de Temperatura

5.1. Modelo Fenomenológico

5.2. Identificación por Curva de Reacción

5.3. PID Horno con Microcontrolador PIC

5.4. PID con PIC en planta Motor-Generador

5.5. PID dentro de un Predictor de Smith con PIC

6. Control PID de Temperatura con Arduino sin Librería

6.1. Control PID Arduino de Temperatura usando Ziegler y Nichols

6.2. Control PI por Cancelación de Polos

6.3. Control PI por Asignación de Polos

6.4. Predictor de Smith

6.5. Anti Windup en un Control PID

6.6. Todo sobre Ziegler Nichols – Sintonia de Control PID

7. Códigos

7.1. Video del Código

7.2. Video de la Implementación

7.3. Descargas

Con lo que vas a aprender en este sitio web, estarás en la capacidad de implementar y programar todo tipo de proyectos de control PID con Arduino o cualquier otro microcontrolador.

Antes de comenzar te hago la invitación para que veas el curso gratuito de Arduino desde cero.

Y que te suscribas al canal de YouTube, si lo que deseas es aprender sobre Arduino y principalmente sobre la teoría del control.

¿Que es el controlador PID?

A nivel industrial el controlador PID es el más popular y más ampliamente difundido, principalmente por su facilidad de entendimiento y la robustez que presenta para poder regular de forma precisa una variable especifica de proceso (temperatura, presión, peso, nivel, etc)

Control PID es la abreviación de Control Proporcional, Integral y Derivativo y son justamente estas tres características que nos permiten controlar y regular las variables de proceso, donde cada parcela aporta una característica diferente y si quieres profundizar un poco en esto, te dejo una lista de 3 videos de control PID que lo explica al detalle.

Algo importante de entender es que el controlador PID actua sobre el error. Donde el error solamente es la diferencia entre el setpoint (referencia deseada por el usuario) y la salida (valor medido por el sensor).

e(k)=r(k)-y(k)

El término P (proporcional) amplifica o atenua la señal del error. Es decir, cuando el sistema presenta un error grande y positivo, la salida de control será proporcionalmente grande y positiva, dado que el error es multiplicado por el factor de ganancia Kp. El término P actua con el error actual (PRESENTE).
El término I (integral) agrega el efecto de memoria al controlador, es decir que tiene en cuenta los valores pasados del error y los integra a lo largo del tiempo. La acción integral elimina el error en estado estacionario, es decir hace que la variable llegue al setpoint. El término I actual con el error anterior (PASADO).
El término D (derivativo) hace una predicción del comportamiento futuro del error. Utilizando para eso una proyección de la linea tangente al punto actual del error. El termino D estima el error futuro del error (FUTURO).

Control PID en Arduino

Para comenzar a entender como funciona un controlador PID, inicialmente, vamos a ver su representación clásica en el siguiente diagrama de bloques:

Notemos que las señales del diagrama anterior esta representado en el tiempo por muestras k (lo explicaré más adelante) y las funciones del controlador y el proceso C(z) y P(z) en función de la variable compleja z, eso nos indica que estamos hablando de un control digital que actúa por instantes de muestreo.

donde r(k) es nuestra señal de referencia o set point, e(k) es nuestra señal de error (La resta entre r(k) y y(k)), C(z) es nuestro controlador PID de temperatura discreto, u(k) es nuestra señal de control (Ley de control), P(z) es nuestra planta o proceso en representación discreta que deseamos controlar, y(k) es nuestra variable de salida la cual es leída por el sensor del proceso.

Podrán observar en la literatura que la ley de control PID en el caso continuo es representarse por la siguiente ecuación:

u(t)=k_pe(t)+\dfrac{k_p}{t_i}\int_{0}^{t}e(t)dt+k_pt_d\dfrac{de(t)}{dt}

El control PID posee tres parámetros ( $k_p,t_i,t_d$ ) correspondientes a la ganancia proporcional, tiempo integral y tiempo derivativo respectivamente. Si quieres profundizar como funcionan esos tres componentes, te dejo 3 videos que explican en detalle cada uno de los parámetros del control PID.

Existen numerosas técnicas y autores que muestran formas de sintonizar o ajustar los parámetros del controlador, que no es nada trivial. En esta entrada, les voy a enseñar TRES formas diferentes de sintonizar este controlador:

Sintonia por Ziegler y Nichols
Control por Cancelamiento de Polos
Control por Asignación de Polos

Sin embargo, en este caso como vamos a realizar la implementación del control PID en Arduino, vamos a representar la ecuación de la ley de control en su forma discreta o digital, que represente el diagrama visto anteriormente.

Antes de continuar, me gustaría invitarte a alguno de mis cursos premium donde te enseño a implementar varias estrategias de control dentro del Arduino o incluso dentro de un microcontrolador PIC, todo paso a paso.

Curso de Sistemas de Control en Dispositivos Microcontrolados en UDEMY (PIC y ARDUINO)
Certificado de Aprobación una vez finalices el Curso
DESCUENTO si accedes directamente con los siguientes botones de acceso.
NOTA: Si buscas el curso directamente en UDEMY o si lo adquieres en otra plataforma distintas a las mostradas anteriormente NO OBTENDRÁS NINGUN DESCUENTO sobre el valor final del Curso.

Curso Implementado en ARDUINO

Matricularse al Curso

Curso Implementado en Microcontrolador PIC

Matricularse al Curso

Controlador PID Discreto en Arduino

El control discreto PID se obtiene discretizando la ecuación continua vista anteriormente aproximando el término integral mediante la sumatoria trapezoidal y el término derivativo mediante la diferencia de dos puntos asi:

\int e(t)dt = \sum\left[ \dfrac{e(k)+e(k-1)}{2}\right]T_s

\dfrac{de(t)}{dt}=\dfrac{e(k)-e(k-1)}{T_s}

Donde $T_s$ se conoce como el tiempo de muestreo, que es el tiempo a cada cuanto se va a ejecutar la ley de control discreta.

Note que como estamos trabajando en muestras k, eso quiere decir que nuestro error representado por la variable e significa lo siguiente:

e(k) es el error en el instante actual, o tiempo de muestreo actual (presente)
e(k-1) es el error en un instante anterior, o en el tiempo de muestreo anterior (pasado)

Suscríbete a este sitio WEB para estar enterado de las nuevas entradas!

Por otro lado, es de vital importancia saber escoger adecuadamente el periodo de muestreo $T_s$ al momento de querer implementar controladores digitales, para esta entrada vamos a utilizar un método rápido para la selección del periodo de muestreo.

Para eso, voy a suponer que en lazo cerrado, es decir cuando el controlador PID esté actuando sobre la planta, la planta se va a estabilizar rápidamente, aproximadamente en $t_{ss} = 150s$ entonces puedo escoger mi periodo de muestreo en el siguiente intervalo

$\dfrac{t_{ss} }{20}\leq T_s\leq\dfrac{t_{ss} }{10}$

Para nuestro caso del control PID de temperatura con Arduino escogeremos un $T=8s$ , dado que esta en el intervalo $7.5\leq T_s \leq 15$ .

Los parámetros de ajuste del controlador PID de temperatura que vamos a implementar en Arduino los vamos a estimar usando tres estrategias diferentes a partir de los parámetros continuos $k_p,\tau_i,\tau_d$ .

Para este caso vamos a tomar el retardo de tiempo de nuestro modelo continuo como:

\theta = L +T_s/2

en donde $T_s/2$ es una aproximación correspondiente al retardo introducido por el muestreador y el retenedor, recordando que $T_s$ es el período de muestreo.

El control discreto PID se obtiene discretizando la ecuación continua (vista al comienzo de esta entrada) de esa forma obtener la función de transferencia pulso del controlador PID digital:

C(z^{-1})=\dfrac{u(k)}{e(k)}=\dfrac{q_0+q_1z^{-1}+q_2z^{-2}}{1-z^{-1}}

donde:

q_0=k_p\left [ 1+\dfrac{T_s}{2t_i}+\dfrac{t_d}{T_s} \right ]

q_1=-k_p\left [ 1-\dfrac{T_s}{2t_i}+\dfrac{2t_d}{T_s} \right ]

q_2=\dfrac{k_pt_d}{T_s}

Con esto, la ley de control que vamos a ingresar a nuestro PIC sale del control PID discreto en Arduino (Despejando u(k))

u(k)(1-z^{-1})=q_0e(k)+q_1z^{-1}e(k)+q_2z^{-2}e(k)

u(k)-u(k)z^{-1}=q_0e(k)+q_1z^{-1}e(k)+q_2z^{-2}e(k)

u(k)=u(k)z^{-1}+q_0e(k)+q_1z^{-1}e(k)+q_2z^{-2}e(k)

Aplicando transformada inversa Z obtenemos la ecuación en diferencias:

u(k)=u(k-1)+q_0e(k)+q_1e(k-1)+q_2e(k-2)

Así, u(k) quiere decir la ley de control actual, u(k-1) es la ley de control un instante de muestreo atrás, e(k) es el error actual (Referencia – temperatura), e(k-1) es el error un instante de muestreo atrás, e(k-2) es el error dos instantes de muestreo atrás.

Como ves, el implementar tu propio controlador PID será fácil y ya lo verás más adelante cuando te muestre como programar un PID Sencillo con Arduino.

Medidor de Nivel de Agua por Presión con Arduino

Modelo Matemático de un Sistema Térmico

Relevador con Arduino

Planta de Temperatura

Para esta práctica vamos a utilizar la siguiente planta de temperatura la cual es una Shield de Arduino diseñada y proyectada por el Profesor John D. Hedengren de la universidad de Brigham Young University.

Laboratorio de Control de temperatura con Arduino

Basicamente en lo que consiste el sistema es en inyectar corriente al transistor para calentarlo y medir su temperatura con un sensor.

Información detallada sobre esta placa, como modelos matemáticos, controles clásicos y avanzados implementados en Matlab, Simulink y Python pueden ser encontrados en la pagina del profesor John D. Hedengren o en su canal de YouTube: La página es APMonitor.

La placa es distribuida oficialmente en Amazon:

Comprar en Amazon

Un esquema electrónico puede verse directamente desde la página de APMonitor (Click aqui)

Mas o menos el esquema para un transistor es el siguiente, para poner dos transistores es solo duplicar.

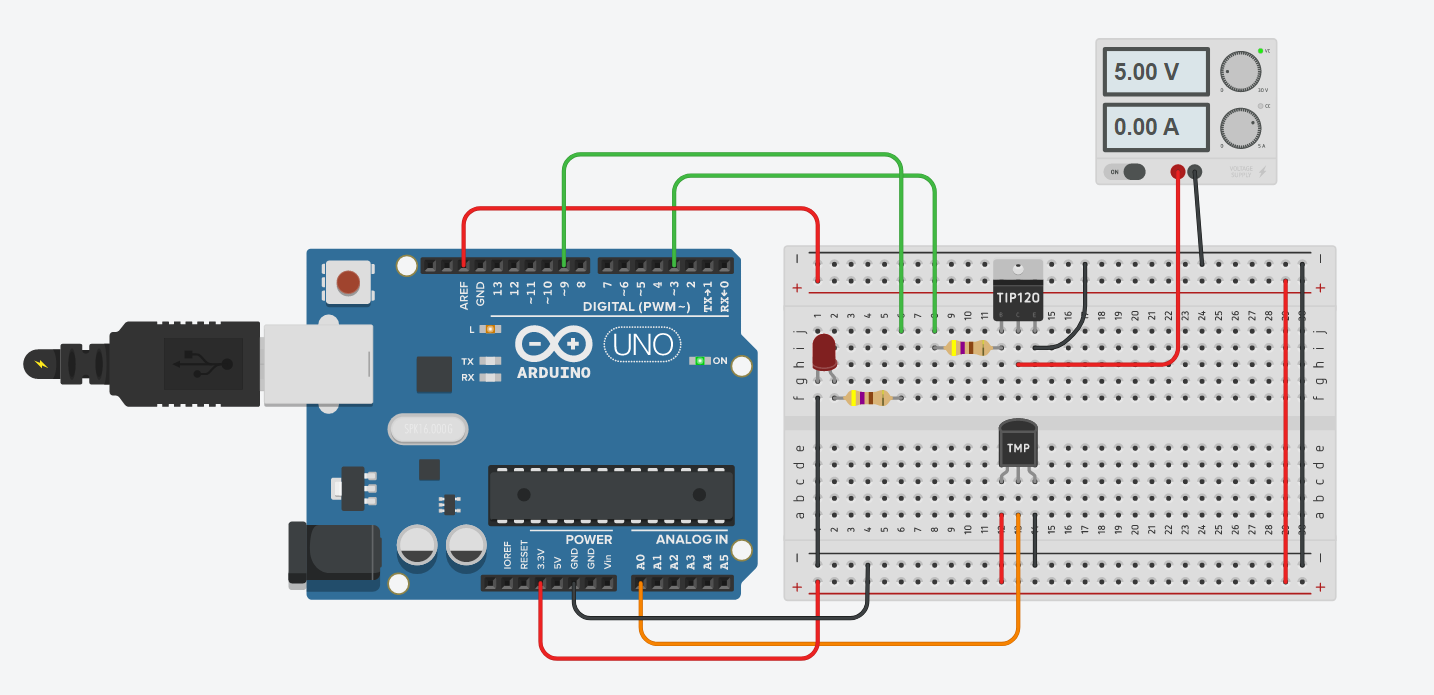
Es importante tener una fuente de alimentación a parte para energizar el transistor. Los componentes reales de la placa son:

Transistor TIP31C (o un reemplazo que pueden ser: BDT31C, MJF31C, MJF31CG, TIP31CF, TIP31CG, TIP31D, TIP31E or TIP31F)
2 Resistencias de 470 Ohms
Sensor de Temperatura TMP36
Led
Jack de alimentación de 5 – 12 VDC

Los tres elementos importantes para un lazo de control son el dispositivo de medición (sensor de temperatura del termistor), un actuador (voltaje al transistor) y la capacidad de realizar un control computarizado (interfaz USB). A la salida máxima, el transistor disipa 3,1 W de potencia con un voltaje de 8,9 V y una corriente de 0,35 A. El calor generado por el transistor se transfiere por radiación, convección y conducción al sensor de temperatura.

El diseño del compensador PID que vamos a realizar con este laboratorio de temperatura puede ser extendido a cualquier otra planta. Por ejemplo, puedes realizar un control PID de temperatura de un horno usando Arduino siguiendo los mismos pasos de este post.

Identificación del Modelo de la Planta de Temperatura

Para poder diseñar un controlador de Temperatura PID digital con arduino será importante entender el funcionamiento del proceso que deseamos controlar, en este caso deberemos caracterizar el modelo matemático de nuestro sistema de temperatura para eventualmente poder realizar el control PID.

Existen várias estrategias para obtener la función de transferencia de los sistemas, en este caso vamos a ver dos métodos distintos:

Realizando el modelo fenomenológico con leyes físico-químicas.
Realizando una identificación de sistemas a través de la curva de reacción.

Modelo Fenomenológico

Para este caso vamos a valernos de las leyes termodinámicas para obtener un modelo matemático NO lineal del sistema y posteriormente realizaremos una linealización del sistema usando las series de Taylor.

El modelo matemático de un sistema térmico (click) (hornos, estufas, calderas, refrigeradores, etc) ya fue visto aquí en el sitio web y fue explicado en detalle junto con su video, por eso recomiendo ver esa entrada si deseas entender el modelo matemático de la planta de temperatura con arduino.

Básicamente en este modelo estamos considerando dos mecanismos principales: convección y radiación, con lo cual se obtiene la siguiente ecuación.

mc_p\dfrac{d T}{d t}=\alpha Q_i+UA(T_{\infty}-T)+\epsilon \sigma A (T_{\infty}^4-T^4)

donde el calor específico es $c_p$ , la masa es $m$ , el cambio en temperatura es $(T-T_{ref})$ , U es el coeficiente de transferencia de calor, A es el área, T es la temperatura del transistor, $T_\infty$ es la temperatura del ambiente, ϵ es la emisividad, σ es la constante de Stefan-Boltzmann

Los parámetros del modelo fueron tomados de la pagina de APMonitor, modificando el coeficiente de transferencia de calor y el factor del calentador para Mi caso específico:

Quantity	Value
Temperatura inicial (T0)	296.15 K (23^oC)
Temperatura Ambiente (T∞)	296.15 K (23^oC)
Salida del Calentador (Q)	0 to 1 W (0%-100%)
Factor del Calentador (α)	0.014 W/(% heater)
Capacidad Calorifica (C_p)	500 J/kg-K
Area de la superficie (A)	1.2×10^-3 m² (12 cm²)
Masa (m)	0.004 kg (4 gm)
Coeficiente de transferencia de calor(U)	5 W/m²-K
Emisividad (ε)	0.9
Stefan Boltzmann Constant (σ)	5.67×10^-8 W/m²-K⁴

La función de transferencia obtenida después de linealizar el modelo fue:

G(s)=\dfrac{1.127e^{-10 s}}{160 s + 1}

La comparación del modelo lineal, no lineal y la planta real se ve a continuación:

Identificación por Curva de Reacción

Este tipo de caracterizar una planta es una de las más usadas experimentalmente y aquí ya lo hicimos várias veces en las siguientes 3 entradas:

PID Horno con Microcontrolador PIC

PID con PIC en planta Motor-Generador

PID dentro de un Predictor de Smith con PIC

La idea en este punto es poder aproximar nuestro modelo con una función de transferencia de primer orden con retardo el cual tiene la siguiente forma:

G(s)=\dfrac{Ke^{-L s}}{\tau s +1}

Para este experimento, vamos a inyectar al transistor el 40% del PWM del Arduino y esperamos hasta que el transistor caliente y se estabilice la temperatura. Podemos utilizar el serial ploter para ver la respuesta o pueden diseñar un programa para enviar los datos al computador.

/******************************************************
 * ****************************************************
 * ****  CURVA DE REACCIÓN DE TEMPERATURA         *****
 * ****  By: SERGIO ANDRES CASTAÑO GIRALDO        *****
 * ****  https://controlautomaticoeducacion.com/  *****
 * ****                                           *****
 * ****************************************************
 */
// Definiciones componentes de la tarjeta
#define sensor1 A0  //TMP36
#define sensor2 A2  //TMP36
#define heater1 3   //TIP31C
#define heater2 5   //TIP31C
#define hot     9   //Led
//Variables Globales
float T1,aux;       //Temperatura del Heater 1
void setup() {
  pinMode(hot,OUTPUT);  //Led "Caliente" como salida
  digitalWrite(hot,LOW);
  analogReference (EXTERNAL); //Referencia analógica PIN AREF (3,3v) 
  //Configuramos el puerto serial
  Serial.begin(9600);
}
void loop() {
  int i;
  //Filtro de promedio movil en la lectura ADC
  aux=0;
  for(i=0;i<10;i++){
    aux = aux + (float(analogRead(sensor1))*3.3/1023.0-0.5)/0.01; //TMP36
    //delay(5);
  }
  T1 = aux/10.0;
 analogWrite(heater1,255*0.4);
 //Usar el Serial Plotter
    Serial.println("Temperatura_1");
    Serial.print(T1);
    delay(1000);
}

La curva de reacción del experimento para un tiempo de 600 segundos fue:

En este caso podría haberse dejado más tiempo para ver mejor el tiempo de estabilización, $T_{ss}$ , sin embargo vamos a establecer los 600 segundos como el tiempo estable. Asi podemos encontrar la constante de tiempo $\tau$ , que es simplemente tomar el tiempo de estabilización y dividirla por 4:

\tau=\dfrac{T_{ss}}{4}=\dfrac{600}{4}=150

Vemos que la gráfica comienza en 25°C y llega hasta 61°C y que para conseguir esta respuesta tuvimos que colocar en un 40% el PWM del Arduino. Así podemos obtener la ganancia del proceso con la siguiente formula:

K=\dfrac{T_{final}-T_{inicial}}{U_{final}-U_{inicial}}

K=\dfrac{61-25}{40-0}=0.9°C/\%

Con un poco más de tiempo en el experimento, intuyo que la ganancia nos daría un poco mayor.

Por otro lado el retardo de tiempo puede obtenerse de la gráfica y corresponde al tiempo que demora la temperatura en comenzar a responder después de haber inyectado el escalón del 40% en el PWM.

Haciendo un ZOOM en la gráfica vemos lo siguiente:

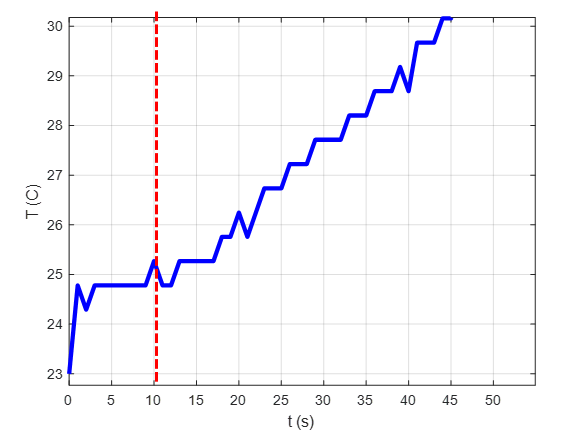
La primera medida en 23 se desconsidera porque fue un valor que forcé en mi interfaz gráfica. Vemos que la temperatura se mantiene en la temperatura ambiente (aprox 25C) y solo comienza a subir mas o menos a los 10 – 12 segundos. entonces definimos nuestro retardo $L=10$

De esa forma nuestra función de transferencia por curva de reacción nos dio:

G(s)=\dfrac{0.9e^{-10 s}}{150 s + 1}

La comparación del modelo con los datos real se muestra a continuación:

Indentificación de Modelo de Temperatura

Control PID de Temperatura con Arduino sin Librería

Como ya tenemos determinada la dinámica de nuestra planta de temperatura, podemos proceder a la realización de nuestro sistema de control en lazo cerrado.

El termostato que implementaremos usará un PID con TMP36 como sensor, pero también puede ser usado un PID con LM35 como elemento de sensado.

Para el cálculo de los parámetros del control PID de Temperatura con Arduino y Matlab vamos a usar la función de transferencia del modelo fenomenológico.

A continuación se describe detalladamente como implementar un termostato PID con Arduino sin usar librerías.

Control PID Arduino de Temperatura usando Ziegler y Nichols

Todo lo que necesitas saber sobre la estrategia de sintonia de Ziegler y Nichols fue tratado en otra entrada con video incluido.

Vamos a usar la siguiente tabla para la sintonia del controlador pid de temperatura con arduino:

A continuación se muestra la respuesta del sistema y se compara con la respuesta simulada del sistema. Donde se evidencia que es fácil implementar un pid para control de temperatura en arduino.

De la respuesta anterior, podemos ver como la sintonia por Ziegler y Nichols consigue llevar la temperatura a la referencia de 40C, adicionalmente podemos comparar que la respuesta simulada es bastante próxima con la respuesta real del sistema, mostrando la importancia de la simulación de los procesos para el entendimiento y análisis de los sistemas.

Control PI por Cancelación de Polos

El control PI por cancelación de polos cancela el polo de la planta con el parámetro integral del controlador.

Seleccionamos una constante de tiempo deseada. Por ejemplo, seleccionamos una constante de tiempo de 45 segundos para que se estabilice el proceso en más o menos 180 segundos (ya sabemos que el tiempo de estabilización es 4 veces la constante de tiempo)

\tau_{s}=45

se calcula la ganancia proporcional del control PI:

k_p=\dfrac{\tau}{K\tau_s}=\dfrac{160}{1.04*45}=3.4188

se calcula el tiempo integral del control PI:

t_i=\tau

A continuación se muestra la respuesta del sistema y se compara con la respuesta simulada del sistema.

Cancelamiento de Polos en el PID con Arduino

Una vez más podemos ver como la respuesta simulada es próxima a la respuesta real del sistema, observamos también que el control consigue llevar la variable a la referencia, sin embargo el control no es muy efectivo debido a su dependencia del modelo.

En este caso, requerimos estimar correctamente la ubicación del polo para poder cancelarlo con el controlador, claramente esto en la práctica es muy complicado, debido al grado de incerteza que se tiene al momento de estimar el modelo.

Control PI por Asignación de Polos

La técnica del PI por Asignación de Polos fue explicada en detalle en otra entrada.

En este proyecto de controlador solo utilizamos nuestra parcela Proporcional y integral, colocando la acción derivativa en cero.

La idea básica de este diseño es asignarle polos a nuestro proceso para que actúe de la manera como nosotros deseamos:

Seleccionamos una tiempo de establecimiento deseado. Es decir el tiempo en que queremos que se estabilice la temperatura, por ejemplo, vamos a suponer que nosotros queremos que la temperatura se estabilice en más o menos 220 segundos:

T_{ss}=220

Definimos un factor de amortiguamiento con el fin de aproximar nuestro sistema a una dinámica subamortiguada de segundo orden.

\zeta=0.6901

Calculamos la frecuencia natural de nuestro sistema a fin que nuestro sistema se estabilice con el criterio del 2%

W_n=\dfrac{4}{\zeta T_{ss}}=\dfrac{4}{151.8235}=0.0263

Calculamos el polinomio deseado el cual contiene los dos polos complejos conjugados que estamos asignando al sistema, para eso usamos los coeficientes 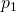$p_1$ y $p_2$ del polinomio de segundo orden:

s^2+p_1s+p_2=s^2+2\zeta W_ns+Wn^2

p_1=2\zeta W_n=0.0364

p_2=W_n^2=6.9413\cdot10^{-4}

Donde los polos son:

s_{1,2}=-0.0182 \pm j0.0191

Por ultimo calculamos el parametro kc y ti con las siguientes formulas:

k_p=\dfrac{P_1\tau-1}{K}=4.6329

t_i=\dfrac{k_pK}{P_2\tau}=43.3832

A continuación se muestra la respuesta del sistema y se compara con la respuesta simulada del sistema.

Asignación de Polos Control PID Arduino Temperatura

Podemos observar nuevamente como concuerdan las dinámicas simuladas con las dinámicas reales.

En este caso el control consiguió llevar nuevamente la variable a la referencia en el tiempo establecido.

Adicionalmente, podemos recalcular el controlador por asignación de polos para por ejemplo hacer que el sistema tenga un tiempo de establecimiento mucho más lento, por ejemplo de $T_{ss}=640$ segundos. Esta respuesta puede ser observada a continuación:

Asignación de Polos control lento — Asignación de Polos Control Lento PID Arduino

Predictor de Smith

Anti Windup en un Control PID

Todo sobre Ziegler Nichols – Sintonia de Control PID

Códigos

A continuación dejo disponibles los códigos del Control PID Arduino sin librería de Temperatura y de la interfaz gráfica en Matlab. Recuerda compartir este contenido para permitir que este sitio web siga creciendo y aportando contenido de valor.

Video del Código

Video de la Implementación

Descargas

Para el control pid con arduino de temperatura puedes usar el siguiente código:

Descargar Código de Arduino + Interfaz en Matlab

/******************************************************
 * ****************************************************
 * ****  CONTROL PID DE TEMPERATURA               *****
 * ****  By: SERGIO ANDRES CASTAÑO GIRALDO        *****
 * ****  https://controlautomaticoeducacion.com/  *****
 * ****                                           *****
 * ****************************************************
 */
#include <TimerOne.h> 
// Definiciones componentes de la tarjeta
#define sensor1 A0  //TMP36
#define sensor2 A2  //TMP36
#define heater1 3   //TIP31C
#define heater2 5   //TIP31C
#define hot     9   //Led
//Variables Globales
float T1,aux;       //Temperatura del Heater 1
float r1=0.0;  //Referencia del Heater 1
volatile float u=0.0,u_1=0.0;    //Acción de Control
byte Ts = 8; //Periodo de muestreo
//Parámetros del PID
float kp,ti,td;
float q0,q1,q2;  
volatile float e=0.0,e_1=0.0,e_2=0.0;
      
float k=1.04,tau=160,theta=10+Ts/2;   //Parámetros del Modelo del sistema
float Tlc,eps,Wn,P1,P2,tau_d;            //Parámetros del diseño por asignación de polos
String dato;
bool Matlab = false; // 0: Usa el Serial Plotter; 1: Usa la interfaz de Matlab
/* Tipo de Control:
 *  1: Control por Asignación de Polos
 *  2: Control por Cancelamiento de polos
 *  3: Control por Ziegler y Nichols
 */
byte type = 3;
/*===========================================================================*/
/*=======================    FUNCION DEL CONTROL PID  =======================*/
/*===========================================================================*/
void PID(void)
{
    
    e=(r1-T1);
    // Controle PID
      u = u_1 + q0*e + q1*e_1 + q2*e_2; //Ley del controlador PID discreto
    
    if (u >= 100.0)        //Saturo la accion de control 'uT' en un tope maximo y minimo
     u = 100.0;
    
    if (u <= 0.0 || r1==0)
     u = 0.0;
     
     
     
     //Retorno a los valores reales
     e_2=e_1;
     e_1=e;
     u_1=u;
     
     //La accion calculada la transformo en PWM
     
     analogWrite(heater1,map(u, 0,100, 0,255));
     
}
//Función del Periodo de Muestreo (Timer 1)
void SampleTime(void)
{
  digitalWrite(hot, !digitalRead(hot)); //Led Toggle
  PID();
}
void setup() {
  pinMode(hot,OUTPUT);  //Led "Caliente" como salida
  digitalWrite(hot,LOW);
  analogReference (EXTERNAL); //Referencia analógica PIN AREF (3,3v)
  //Configuramos el puerto serial
  Serial.begin(9600);
  //Espera 10 segundos en Stand by cuando es energizado la primera vez
  if(!Matlab){
    delay(10000);
    r1=40.0;
  }
    
  //Valor máximo del Timer es 8.3 Segundos
  Timer1.initialize(8000000);      //Configura el TIMER en 8 Segundos
  Timer1.attachInterrupt(SampleTime) ; //Configura la interrupción del Timer 1
  switch (type){
    
  case 1:
  //*************************************************************************//
  //*************  DISEÑO POR ASIGNACIÓN DE 2 POLOS   ****************//
  //*************************************************************************//
   
   Tlc=220.0;                   //Tiempo de establecimiento deseado en Lazo Cerrado 
   eps = 0.6901;                //Factor de Amortiguamiento   
   Wn=4.0/(eps*Tlc);            //Frecuencia natural del sistema
   
   //Ubicación de 2 Polos 
   P1=2.0*eps*Wn;
   P2=Wn*Wn;
   
   kp=(P1*tau-1.0)/k;        //Calculo de Kc
   ti=(k*kp)/(P2*tau);     //Calculo de ti
   td=0.0;
   break;
   
   case 2:
   //*************************************************************************//
   //*****************   DISEÑO POR CANCELACIÓN DE POLOS    *******************//
   //*************************************************************************//
   
   tau_d=45.0;                  //Constante de Tiempo Deseada
   kp=(tau)/(tau_d*k);         //Calculo de Kc
   ti=tau;                   //Calculo de Ti (Igual a la constante de tiempo)
   td=0;
   break;
   case 3:
   //*************************************************************************//
   //*****************   SINTONIA POR ZIEGLER y NICHOLS    *******************//
   //*************************************************************************//
   kp=(1.2*tau)/(k*theta);
   ti=2.0*theta;
   td=0.5*theta;
   break;
  }
   //*************************************************************************//
   //*****************           PID DIGITAL               *******************//
   //*************************************************************************//
  // Calculo do controle PID digital
   q0=kp*(1+Ts/(2.0*ti)+td/Ts);
   q1=-kp*(1-Ts/(2.0*ti)+(2.0*td)/Ts);
   q2=(kp*td)/Ts;
}
void loop() {
  int i,ini=0,fin=0;
  String degC;
  //Filtro de promedio movil en la lectura ADC
  aux=0;
  for(i=0;i<10;i++){
    aux = aux + (float(analogRead(sensor1))*3.3/1023.0-0.5)/0.01; //TMP36
    //delay(5);
  }
  T1 = aux/10.0;
  //T1= (float(analogRead(sensor1))*5.0/1023.0-0.5)/0.01; //TMP36
  if(Matlab){ //Usar la interfaz de Matlab
  //___________________________________________
    if (Serial.available()){
      //leemos el dato enviado
      dato=Serial.readString();
      //Busco el valor del escalon en los datos recibidos
      for(i=0;i<10;i++){
        if(dato[i]=='S'){
          ini=i+1;
          i=10;
        }
       }
       for(i=ini;i<10;i++){
        if(dato[i]=='$'){
          fin=i;
          i=10;
        }
       }
       // salvo en degC el caracter con el escalon
        degC=dato.substring(ini, fin);
      r1 = degC.toInt();   // Convert character string to integers
    }
  //____________________________________________
  
      Serial.print("I");
      Serial.print(T1);
      Serial.print("F");
      Serial.print("I");
      Serial.print(T1);
      Serial.print("F");
  
      Serial.print("C");
      Serial.print(u);
      Serial.print("R");
      Serial.print("C");
      Serial.print(u);
      Serial.print("R");
  }
  else{  //Usar el Serial Plotter
    Serial.println("Temperatura_1,Setpoint_1");
    Serial.print(T1);
    Serial.print(","); 
    Serial.println(r1); 
  }
  
  delay(1000);
}

[cite]

Eso es todo por la entrada del dia de hoy, espero les haya gustado y hayan aprendido algo nuevo. Si te ha servido el contenido de esta entrada, de los videos y los códigos de implementación y deseas apoyar mi trabajo invitandome a un café super barato, puedes hacerlo en el siguiente link:

👉 Invitar a Sergio a un Café ☕️

Que esten muy bien, nos vemos en la siguiente entrada.

Volver al Curso de Arduino

Mi nombre es Sergio Andres Castaño Giraldo, y en este sitio web voy a compartir una de las cosas que mas me gusta en la vida y es sobre la Ingeniería de Control y Automatización. El sitio web estará en constante crecimiento, voy a ir publicando material sobre el asunto desde temas básicos hasta temas un poco más complejos. Suscríbete al sitio web, dale me gusta a la página en Facebook y únete al canal de youtube. Espero de corazón que la información que comparto en este sitio, te pueda ser de utilidad. Y nuevamente te doy las gracias y la bienvenida a control automático educación.