Hola controleros y controleras, en esta entrada daremos una introducción al control fuzzy usando lógica difusa y lo vamos a implementar en Simulink y adicionalmente haremos una implementación real en el laboratorio de temperatura.
Antes de comenzar, te invito a que veas nuestro curso gratuito sobre Control por Realimentación
Y que te suscríbas al canal si te interesa los sistemas de control.
Lógica Difusa
Los inicios de la lógica difusa o borrosa se remontan a la década de los años 60 en California – Estados Unidos cuando el profesor Lofti A Zade publica un trabajo titulado “Fuzzy sets” el cual introduce en el mundo científico la teoría de la lógica difusa, la cual consiste en dar una cantidad múltiple de valores a determinada variable permitiendo así incluir el razonamiento impreciso en el análisis de incertidumbre que pueda presentar dicha variable.
Este estudio de la lógica difusa se basa en la teoría tradicional de los conjuntos. Desde allí se parte para el estudio de un elemento y la forma en que este hace parte, o tiene pertenencia a un conjunto U (universo establecido) que cumple con un número de características o parámetros comunes entre sí para el razonamiento y la lógica humana.
La lógica fuzzy es utilizada cuando se tienen sistemas en los cuales su información no es exacta, sino que contienen un alto grado de imprecisión. Los métodos de esta lógica se basan en conjuntos difusos o también llamados Membership Functions (MF) o funciones de membrecía.
Dichos conjuntos son características expresadas por el experto de forma lingüística que pueden ser nombres o adjetivos y que toman un valor de 0 a 1 dependiendo el grado de pertenencia del conjunto en un universo.
Estas funciones tienen una representación gráfica que responde regularmente a figuras geométricas como formas triangulares o trapezoidales, y también a funciones como las campanas gaussianas, y dentro de sus perímetros se establecen los niveles a los que pertenecen dentro del universo del discurso.
Control Fuzzy
Ebrahim Mamdani fue el encargado de mostrar la aplicación de la lógica difusa en los sistemas de control en 1974, desarrollando el primer control fuzzy práctico para regular un motor de vapor.
Para esta entrada, vamos a ejemplificar el uso del controlador difuso controlando la variable temperatura de nuestro Laboratorio de Temperatura, pero adicionalmente haremos la simulación en Simulink, si tu solamente deseas ver como programar el fuzzy con matlab.
- Curso de Sistemas de Control en Dispositivos Microcontrolados en UDEMY (PIC y ARDUINO)
- Certificado de Aprobación una vez finalices el Curso
- DESCUENTO si accedes directamente con los siguientes botones de acceso.
- NOTA: Si buscas el curso directamente en UDEMY o si lo adquieres en otra plataforma distintas a las mostradas anteriormente NO OBTENDRÁS NINGUN DESCUENTO sobre el valor final del Curso.
En la siguiente figura vamos a mostrar el diagrama de bloques de un control fuzzy el cual implementaremos en esta entrada.
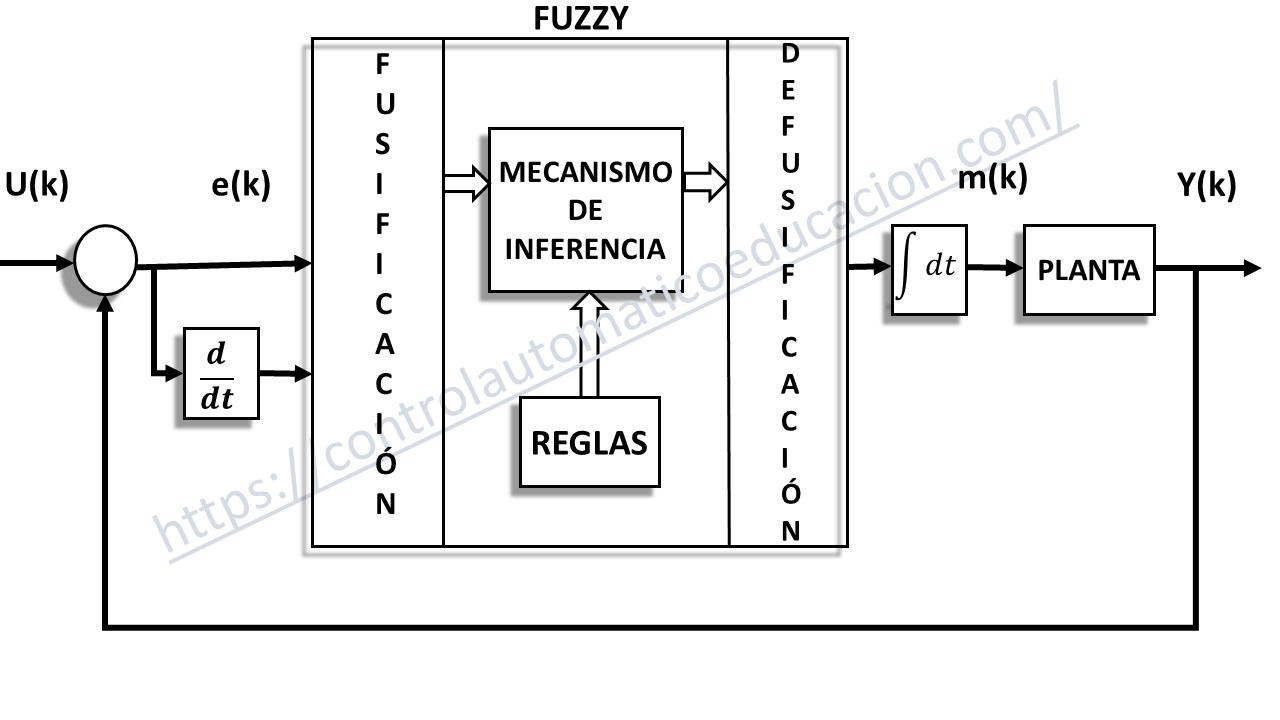
Etapa de Fusificación
En esta etapa se da el proceso de conversión de los valores de entrada de forma lingüística, a valores que el control pueda interpretar.
Universo del discurso
Dentro del control difuso se tiene en cuenta el conocimiento del experto del sistema, los parámetros del error y la derivada del error se extraen los rangos dentro de los cuales se mueven estos dos.
Funciones de pertenencia o membrecías (µ o MF)
Una función de pertenencia es una curva que define el grado, entre uno y cero, en que las variables pertenecen a los conjuntos difusos, se definen según el experto, analizando el sistema a controlar. Toman formas, las más conocidas son: Singlentons, trapezoidales, triangulares, sinoidales, gaussianas, entre otras. Estas funciones toman valores lingüísticos definidos por el mismo experto según el comportamiento de las variables.
Variables lingüísticas de entrada.
Como se muestra en el diagrama de bloques del control fuzzy la primera variable de entrada es el error, debido a que es la diferencia que hay entre el valor de referencia, con los datos de la variable del sistema o proceso.
Para esta variable se va a diseñar siete variables lingüísticas, o particiones del universo del discurso. Las cuales son:
- eNG (Error negativo grande) indica cuando la salida del error está muy por encima del valor de referencia.
- eNM (Error negativo medio) indica cuando la salida del error está medianamente por encima del valor de referencia.
- eNP (Error negativo pequeño) indica cuando la salida del error está por encima pero con muy poca diferencia del valor de referencia.
- eZ (Error cero) indica cuando la salida del error es igual al valor de referencia.
- ePP (Error positivo pequeño) indica cuando la salida del error está por debajo pero con muy poca diferencia del valor de referencia.
- ePM (Error positivo medio) indica cuando la salida del error está medianamente por debajo del valor de referencia.
- ePG (Error positivo grande) indica cuando la salida del error está muy por debajo del valor de referencia.
La otra variable de entrada para el sistema fuzzy es la derivada del error, dicha entrada seria también una integral del error, pero esto implicaría tener un universo del discurso muy amplio, por dicho motivo se opta por usar el diferencial del error para posteriormente integrar la salida del sistema difuso.
Las variables lingüísticas son:
- deNG (Derivada error negativo grande) indica cuando la salida tiene una pendiente positiva.
- deNM (Derivada error negativo mediano) indica cuando la salida tiene una pendiente medianamente positiva.
- deNP (Derivada error negativo pequeño) indica cuando la salida tiene una pendiente positiva casi constante.
- deZ (Derivada error cero) indica cuando la salida permanece constante.
- dePP (Derivada error positivo pequeño) indica cuando la salida tiene una pendiente negativa casi constante.
- dePM (Derivada error positivo mediano) indica cuando la salida tiene una pendiente medianamente negativa.
- dePG (Derivada error positivo grande) indica cuando la salida tiene una pendiente negativa.
Variables lingüísticas de salida
Esta variable describe tanto la salida de potencia del calentador o heater hacia los transistores para controlar temperatura. También se diseñaron siete variables lingüísticas o particiones del universo del discurso, las cuales fueron:
- UFNG (Salida negativa grande) cuando se necesita bajar de manera inmediata la frecuencia del variador o la potencia de la resistencia.
- UFNM (Salida negativa mediana) cuando se necesita bajar de manera rápida la frecuencia del variador o la potencia de la resistencia.
- UFNP (Salida negativa pequeña) cuando se necesita bajar de manera lenta la frecuencia del variador o la potencia de la resistencia.
- UFZ (Salida cero) indica cuando se necesita bajar dejar constante la frecuencia del variador o la potencia de la resistencia.
- UFPP (Salida positiva pequeña) cuando se necesita subir de manera lenta la frecuencia del variador o la potencia de la resistencia.
- UFPM (Salida positiva mediana) cuando se necesita subir de manera rápida la frecuencia del variador o la potencia de la resistencia.
- UFPG (Salida positiva grande) cuando se necesita subir de manera inmediata la frecuencia del variador o la potencia de la resistencia.
Función de pertenencia triangular
Para este control fuzzy serán creadas funciones de pertenencia triangular, representadas por la siguiente figura:

Cuya ecuación viene dada por:
f(x,a,b,c)= \left\{\begin{matrix}
0 & x \leq a\\
\dfrac{x-a}{b-a} & a \leq x \leq b\\
\dfrac{c-x}{c-b} & b \leq x \leq c\\
0 & c \leq x
\end{matrix}\right.Entonces el grado de pertenencia del valor de entrada viene dado por la siguiente ecuación:
f(x,a,b,c)= {\rm max}\left({\rm min} \left(\dfrac{x-a}{b-a}, \dfrac{c-x}{c-b}\right ) , 0\right )Reglas de inferencia
La tarea del sistema de inferencia es tomar los niveles de pertenencia y apoyado en la base de reglas genera una salida en el sistema difuso. La base de reglas es la manera que tiene el sistema difuso de guardar el conocimiento lingüístico que le permiten resolver el problema para el cual ha sido diseñado. Estas reglas son del tipo IF-THEN.
La elaboración de las reglas del sistema difuso se hacen mediante la tabla FAM, la cual involucra todas las combinaciones posibles que puede presentarse en el proceso.
| e/de | deNG | deNM | deNP | deZ | dePP | dePM | dePG |
| eNG | UFNG | UFNG | UFNG | UFNG | UFNM | UFNP | UFZ |
| eNM | UFNG | UFNG | UFNG | UFNM | UFNP | UFZ | UFPP |
| eNP | UFNG | UFNG | UFNM | UFNP | UFZ | UFPP | UFPM |
| eZ | UFNG | UFNM | UFNP | UFZ | UFPP | UFPM | UFPG |
| ePP | UFNM | UFNP | UFZ | UFPP | UFPM | UFPG | UFPG |
| ePM | UFNP | UFZ | UFPP | UFPM | UFPG | UFPG | UFPG |
| ePP | UFZ | UFPP | UFPM | UFPG | UFPG | UFPG | UFPG |
Las reglas son extraídas de la tabla FAM mostrada anteriormente a través de los antecedentes que se enuncian en la primera fila y la primera columna, dando como resultado la intersección entre los antecedentes involucrados, por ejemplo, las tres primeras reglas se constituyen de la siguiente manera:
- If (e is eNG) and (de is deNG) then (u is UFNG)
- If (e is eNG) and (de is deNM) then (u is UFNG)
- If (e is eNG) and (de is deNP) then (u is UFNG)
Etapa de defusificación
En esta etapa se representa por medio de un valor numérico el resultado de los valores arrojados por los grados de pertenencia de las variables de entrada. Se evalúan las reglas de inferencia y se obtiene la respuesta del controlador en términos de cada conjunto de salida.
El método de defusificación utilizado para el diseño del controlador fuzzy, fue el de centro de masa. Este método es el más utilizado para la defusificacion. Es también llamado método de centro de gravedad, el cual retorna el centro del área de la curva o del polígono que se generó en la etapa de inferencia.
Agregación
en la etapa de agregación, se hace uso de la función máximo, el cual toma el valor máximo de todas las reglas que se encuentran asociadas en los siete conjuntos o funciones de pertenencia de la salida. Para entender mejor el concepto en esta etapa, se toma como ejemplo el conjunto de membresía de la salida negativa grande (uFNG) el cual según la tabla FAM, siempre se obtiene una salida negativa grande en las reglas 1, 2, 3, 4, 8, 9, 10, 15, 16 y 22.
uNG=max([r(1:4) r(8:10) r(15:16) r(22) ]);
Saturación
En este paso se hace el recorte de la funciones de salida en los puntos máximos hallados en la agregación, con el objetivo de formar una figura geométrica sólida en la salida.
UFNG(UFNG>=uNG)=uNG; UFNM(UFNM>=uNM)=uNM; UFNP(UFNP>=uNP)=uNP; UFZ(UFZ>=uZ)=uZ; UFPP(UFPP>=uPP)=uPP; UFPM(UFPM>=uPM)=uPM; UFPG(UFPG>=uPG)=uPG
Esta etapa del código se encarga de buscar el valor máximo arrojado por la agregación y recortar el polígono en dicho punto.
Posteriormente se procede a crear el vector fx. En este vector quedan unificadas en las funciones de salida, las reglas implicadas para los determinados valores de entrada con sus respectivas saturaciones.
fx=max([UFNG UFNM UFNP UFZ UFPP UFPM UFPG]')
El concepto de la figura geométrica, se entiende de una mejor manera observando:

Calculo del centro de gravedad (cg).
Para obtener el centro de gravedad se realiza mediante la siguiente formula:
cg = \dfrac{\sum x.f(x)}{\sum f(x)}Donde x es el rango o universo del discurso de la variable de salida. f(x) es el vector hallado anteriormente.

Control Fuzzy en Simulink
A continuación implementaremos un controlador difuso inicialmente simulado en Simulink y posteriormente implementado en el TCLAB – Laboratorio de Control de Temperatura.
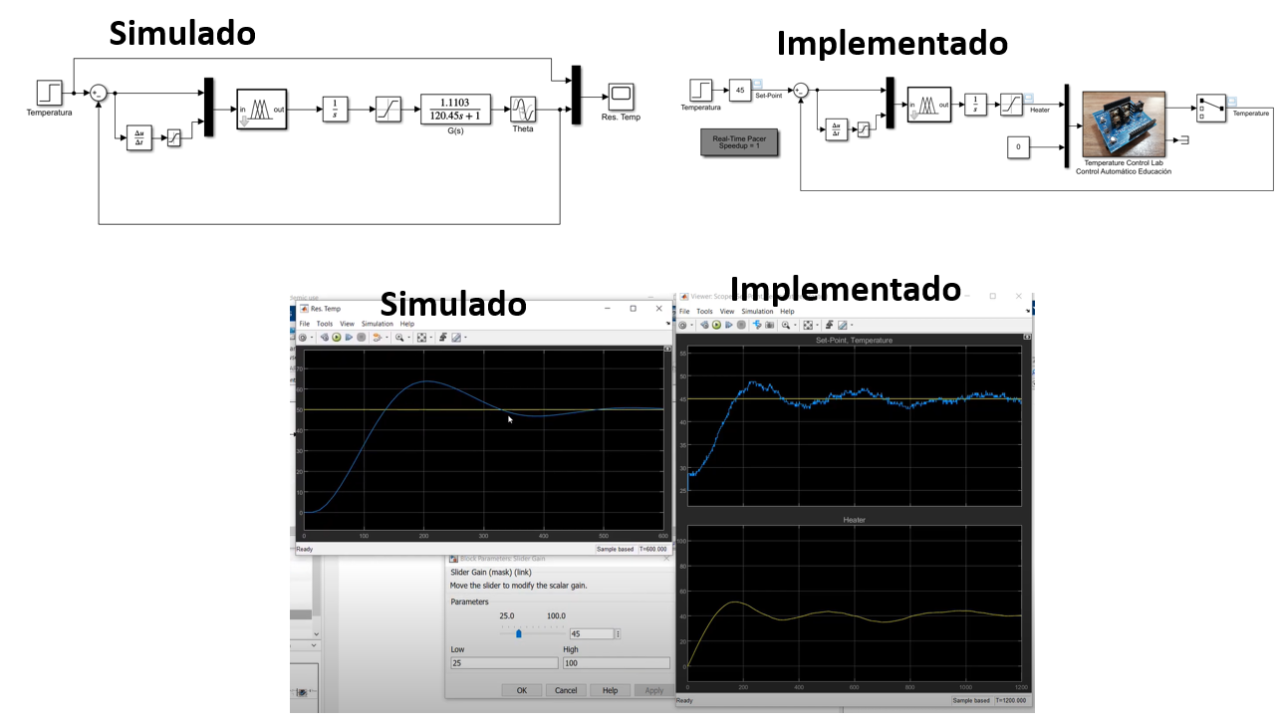
Descargar Archivos
Bibliografia
- Giraldo, S. A. C., Gómez, D. S. H., & Blandón, J. H. G. (2013). Control y monitoreo de temperatura para un horno de curado de prendas índigo utilizando lógica difusa y controles pi. REVISTA POLITÉCNICA, 9(17), 69 – 81. Recuperado a partir de https://revistas.elpoli.edu.co/index.php/pol/article/view/342
- Kovacic, Z., & Bogdan, S. (2006). Fuzzy controller design : Theory and applications (Control engineering (Taylor & Francis) ; 19
- Leonid Reznik, (1997). Fuzzy Controllers Handbook, Newnes.
- Zhang, H., Liu, D. (2006). Fuzzy Modeling and Fuzzy Control. Birkhäuser Basel. p416